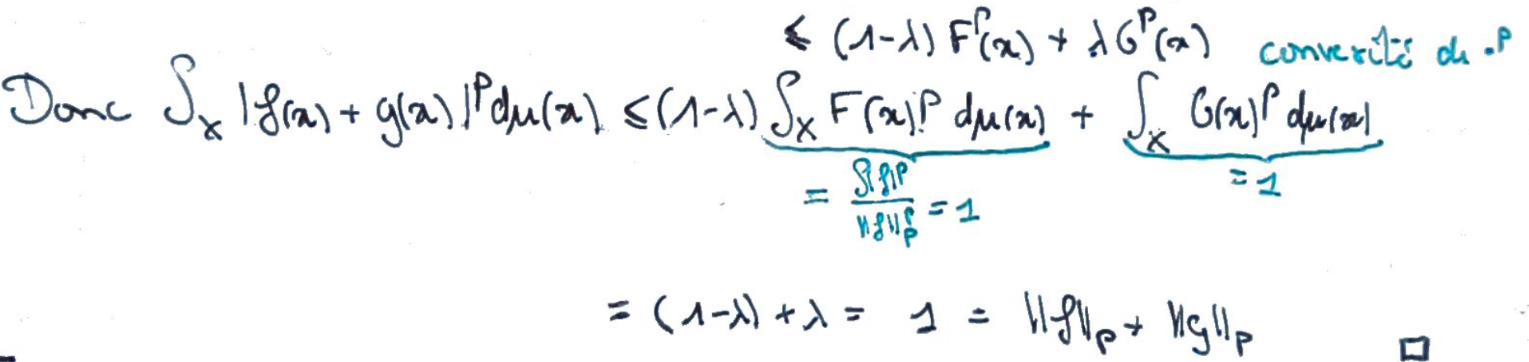Démontrer l'inégalité de Minkowski.
On suppose les fonctions non nulles (cas trivial) et dont la somme des normes vaut \(1\) (par homogénéité).
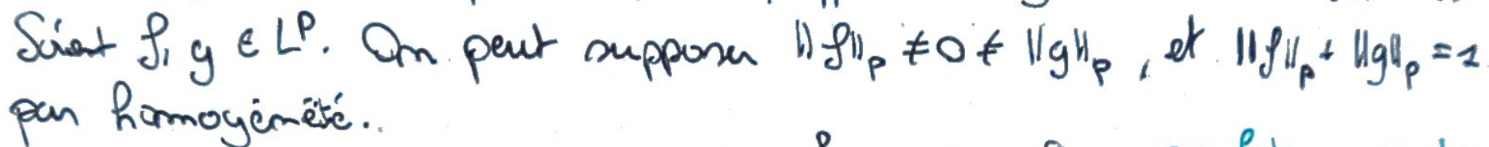
On passe par des fonctions intermédiaires permettant d'écrire une combinaison barycentrique.
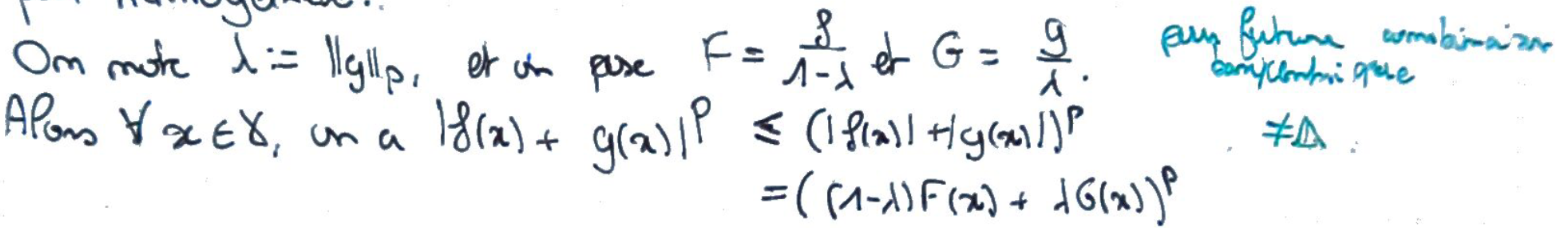
La convexité de \(x\mapsto x^p\) nous donne ensuite le résultat voulu.